Most folk coming into LDI will be familiar with the basics of bonds but on this page I have chosen some of the better explanations I have come across explaining some of the less familiar concepts. To make it easier to know which concepts are covered on this page, I will update the numbered list below before adding the explanation sequentially to this page.
1) Roll down
2) Flatteners, Steepeners, Cost of Carry and the Butterfly
1) Roll Down
When people look at the bond market, the primary focus is on the absolute level of yield when assessing its return potential. Today with the low interest rate environment, people fear that the bond market may not offer enough to meet their investment objective while maintaining a disciplined and certain risk profile during this period of extreme market volatility.
One strategy an astute bond investor can employ in order to enhance returns is to take a total return approach which includes capturing both income and price changes. One such way is to employ a Rolling-Down the Yield Curve Strategy.
Essentially, this is a preferred strategy when the yield curve is upward sloping or steep as in the case of today’s market environment. In particular, an investor will purchase a bond at the top of the steepest part of the yield curve and hold that bond long enough until it reaches a lower yielding part of the curve. In this process and assuming that there is enough duration,the bond that you purchased, coupled with collecting the coupon, will see its price appreciate as it ages with the maturity shortening. After this gain, the bond is sold and the proceeds can be redeployed. So the key to this strategy, all else being equal, is simply time and knowing where to focus.
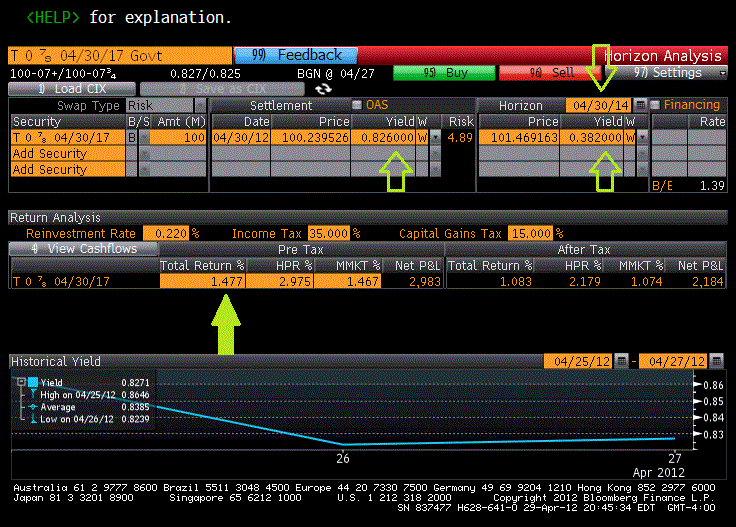
To illustrate the Rolling-Down the Yield Curve strategy, we look at today’s U.S. Treasury Curve. From here we focus on the 5-Year which is yielding 0.826 percent. An investor will purchase that bond at that yield and will hold the bond for a period of time. While held and collecting coupon, the bond’s maturity will shorten. So after two years, that original 5-Year will become a 3-Year bond. Assuming stable interest rates, the yield of that bond will “roll” toward the current 3-Year yield of 0.382 percent. This rolling will in turn, result in price appreciation.

The key to this enhanced strategy is to focus on the part of the maturity spectrum that maximizes the change in yields per the change in maturity assuming there is ample duration. These are the key ingredients to affecting price changes which enhances the income earned from the coupon. Hence, the absolute level of yield as in the case of the Hold-to-Maturity strategy is less of the focus.
So, Rolling-Down the Yield Curve can be utilized on other parts of the yield curve such as from the 7-Year to the 5-Year which has a yield differential of 52 basis points. Similarly, the 10-Year that rolls to the 7-Year has an even greater differential of 59 basis points. Keep in mind that the farther out the maturity, the greater the sensitivity to changes in yield (aka duration) which in turn, increases the risk of the trade.
As an alternative and away from increasing duration, this strategy can be further enhanced by utilizing Corporate Bonds, in either Investment Grade space or the High Yield sectors, which exhibit higher yields (aka spread) than their U.S. Treasury counterparts. As mentioned before, the respective yield curves of the credit sectors need to be upward sloping or steep in order to employ this strategy. (Bondsquawk will cover more in-depth analysis of the corporate bond markets in the coming weeks!)
As with any investment, there are risks. For this particular strategy to produce positive returns, we assume that our yield at the end of our horizon date of two years will be lower than our initial yield at time of entry. In other words, we are betting that yields with maturities that are shorter than our purchased bond (5-Years in our example) will continue to be lower when we exit the trade in two years. So if short term interest rates were to rise within two years, we run the risk of compromising our strategy.
However, given the recent FOMC minutes released last week where Ben Bernanke who continues to battle against high unemployment and headwinds from global debt deleveraging, suggested that U.S. Monetary Policy will continue to be accommodative and short-term interest rates should stay low until late 2014. Furthermore, the recent disappointment in GDP data suggests a slowing economy which in turn, should leave yields on the front end of the curve to remain stable and fairly anchored. As a result, this type of dynamic trading strategy of Rolling-Down the Yield Curve should continue to provide opportunities for enhanced return, despite the low level of interest rates
Essentially, this is a preferred strategy when the yield curve is upward sloping or steep as in the case of today’s market environment. In particular, an investor will purchase a bond at the top of the steepest part of the yield curve and hold that bond long enough until it reaches a lower yielding part of the curve. In this process and assuming that there is enough duration,the bond that you purchased, coupled with collecting the coupon, will see its price appreciate as it ages with the maturity shortening. After this gain, the bond is sold and the proceeds can be redeployed. So the key to this strategy, all else being equal, is simply time and knowing where to focus.
To illustrate the Rolling-Down the Yield Curve strategy, we look at today’s U.S. Treasury Curve. From here we focus on the 5-Year which is yielding 0.826 percent. An investor will purchase that bond at that yield and will hold the bond for a period of time. While held and collecting coupon, the bond’s maturity will shorten. So after two years, that original 5-Year will become a 3-Year bond. Assuming stable interest rates, the yield of that bond will “roll” toward the current 3-Year yield of 0.382 percent. This rolling will in turn, result in price appreciation.

Bond Trading – U.S. Treasury Curve
To quantify this, we turn to using horizon analysis for the current 5-Year U.S. Treasury which is shown in the illustration below. As you can see we purchased the bond at a yield of 0.826 percent or a dollar price of 100.2395. For 100,000 face amount, the total proceeds including accrued income equates to $100,240. Assuming that rates are stable during our time horizon of 2-Years or ending April 30, 2014, we plug in today’s 3-Year yield of 0.382 percent. Again we know that in two years our original 5-Year will become a 3-Year and hence assuming stable interest rates, we can use the aforementioned yield. This yield at this horizon date will correspond to a price of 101.4692. This dollar price which we plan to monetize by selling in the open markets equates to total proceeds of $103,222 or a profit of $2,983. Given our reinvestment rate of 0.22 percent for coupon payments earned during that time period, this profit results in a holding period return of 2.98 percent or 1.48 percent annualized gain. Now, when we compare this gain to a static Hold-to-Maturity strategy we can see the effectiveness of Rolling-Down the Yield Curve.
Bond Trading – Rolling Down the Yield Curve
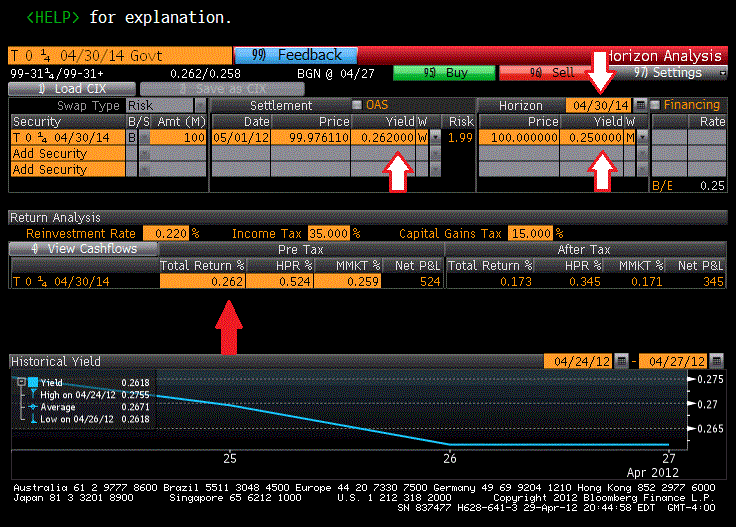
Below, we use the same horizon analysis on owning a 2-Year security with the intent of holding it until maturity. Here, we purchased the current 2-Year U.S. Treasury at a yield of 0.262 percent or a dollar price of 99.9761 for total proceeds of $99,977. Given that the bond will mature in two years at par, the total proceeds earned including coupon payments and reinvestment income will be $100,501 or a gain of just $524. As you would expect from the yield at time of purchase, this gain equates to a holding period return of 0.52 percent or 0.26 percent annualized gain.
Bond Trading – Hold-to-Maturity
Comparatively, the Rolling-Down the Yield Curve strategy outperforms the Hold-to-Maturity Strategy by $2,459 or by an additional return of 1.22 percent on an annualized basis.The key to this enhanced strategy is to focus on the part of the maturity spectrum that maximizes the change in yields per the change in maturity assuming there is ample duration. These are the key ingredients to affecting price changes which enhances the income earned from the coupon. Hence, the absolute level of yield as in the case of the Hold-to-Maturity strategy is less of the focus.
So, Rolling-Down the Yield Curve can be utilized on other parts of the yield curve such as from the 7-Year to the 5-Year which has a yield differential of 52 basis points. Similarly, the 10-Year that rolls to the 7-Year has an even greater differential of 59 basis points. Keep in mind that the farther out the maturity, the greater the sensitivity to changes in yield (aka duration) which in turn, increases the risk of the trade.
As an alternative and away from increasing duration, this strategy can be further enhanced by utilizing Corporate Bonds, in either Investment Grade space or the High Yield sectors, which exhibit higher yields (aka spread) than their U.S. Treasury counterparts. As mentioned before, the respective yield curves of the credit sectors need to be upward sloping or steep in order to employ this strategy. (Bondsquawk will cover more in-depth analysis of the corporate bond markets in the coming weeks!)
As with any investment, there are risks. For this particular strategy to produce positive returns, we assume that our yield at the end of our horizon date of two years will be lower than our initial yield at time of entry. In other words, we are betting that yields with maturities that are shorter than our purchased bond (5-Years in our example) will continue to be lower when we exit the trade in two years. So if short term interest rates were to rise within two years, we run the risk of compromising our strategy.
However, given the recent FOMC minutes released last week where Ben Bernanke who continues to battle against high unemployment and headwinds from global debt deleveraging, suggested that U.S. Monetary Policy will continue to be accommodative and short-term interest rates should stay low until late 2014. Furthermore, the recent disappointment in GDP data suggests a slowing economy which in turn, should leave yields on the front end of the curve to remain stable and fairly anchored. As a result, this type of dynamic trading strategy of Rolling-Down the Yield Curve should continue to provide opportunities for enhanced return, despite the low level of interest rates
2) Flatteners, Steepeners, Cost of Carry and a Butterfly
2.1) Flatteners (Steepeners)
Changes in the shape of the yield curve will change the relative price of bonds represented by the curve. For example, suppose you have a steeply upward sloping yield curve Like the one below:
On this curve the 2-year bond is yielding 0.86% and the 30-year is yielding 4.50%- a spread of 3.64% (4.50% minus 0.86%). This may lead a trader to feel that either:
1) the 30-year was cheap relative to the 2-year. In this case the price of the 30-year is expected to rise by more relative to the 2-year. The corollary is that the yield of the 30-year is expected to fall by more relative to the 2-year yield.
2) the 30-year was going to cheapen even further relative to the 2-year. In this case the price of the 30-year is expected to fall by more relative to the 2-year. The corollary is that the yield of the 30-year is expected to rise by more relative to the 2-year yield.
In the first (second) case the trader is expecting the yield curve to "flatten" ("steepen"). In this case he could simultaneously buy (sell) the 30-year bond and sell (buy) the 2-year bond. By "flatten" ("steepen") we mean that the yield spread, calculcated by subtracting the yield on the shorter maturity bond (the 2-year bond) from the yield on the longer-maturity bond (the 30-year bond), falls (rises). In our example, we measured the yield spread as 3.64% or 364bps (bps = basis points, where 100bps = 1%), and so we are expecting this to decline (increase) to something less (more) than 364bps. It is worth noting that a flattening (steepening) could occur even if 30-year yields rose (fell), all that would be needed would be for 2-year yields to rise (fall) by more than the rise (fall) in 30-year yields.
Why would the trader execute two simultaneous trades rather than simply buying (selling) the 30-year or selling (buying) the 2-year? Because if the yield curve flattens (steepens), reducing (increasing) the spread between the 2-year and the 30-year, it could be the result of
i)) the price of the 2-year falling (rising), or
ii) the price of the 30-year increasing (decreasing), or
iii) a combination of the two.
For the trader to profit from just buying (selling) the 30-year, they would be betting that the flattening (steepening) of the curve will be the result of the price of the 30-year going up (down). Similarly, if the trader sells (buys) the 2-year they are betting that the price of the 2-year will decline (rise). If they take both positions, they do not have to know in what way the general level interest rates will move in order to make a profit - they need only have a view on the relative movements between the 2-year yield and the 30-year yield. Such trades are “market neutral” in the sense that they are not dependent on the market going up or down in order to make a profit.
What do we mean by "market neutral"?
Professional bond traders structure their strategic yield curve trades to be market neutral (also referred to as duration neutral) as they only want to capture changes in relative rates along the curve and not changes in the general level of interest rates. Because longer maturity bonds are more price-sensitive than shorter term bonds (i.e. they have a higher duration), traders do not buy and sell the short-term bonds and long-term bonds in equal amounts of cash; rather they weight the positions based on the relative level of price sensitivity of the two treasuries. This weighting of the positions is known as the hedge ratio.
While there are different ways to measure the price sensitivity of a bond, most traders use the measure PV01, which measures the price change that a bond will experience with a 1 basis point change in interest rates. For example, if the PV01 of a 2-year bond is £0.0217, and the PV01 of a 30-year is £0.1563, the hedge ratio would be 0.1563/0.0217, or 7.2028 to 1.
For a flattener (steepener) trade then every £1,000,000 of cash the trader uses to buy (sell) the 30-year, he would sell (buy) £7,203,000 of the 2-year bond. As interest rates change, the trader would recalculate the PV01 of each bond and adjust the positions accordingly.
2.2 ) Cost of Carry
Changes to the relative yields of the bonds in a strategic curve trade are not the only determining factor to a trades profit or loss. The trader will receive the coupon interest in the bond that they are long, but will have to pay the coupon interest on the bond that they borrowed to sell short. If the interest income received from the long position is greater than the income paid on the short position, the profit is enhanced, if the interest paid exceeds that which is received the profit is reduced, or the loss is increased.
When a trader goes long the short end of the curve and shorts the long end, the proceeds of the short is not sufficient to cover the long position, so the trader will have to borrow funds to purchase the long position. In our steepener example above, the trader sold £1,000,000 of 30-year bonds but needed to buy £7,203,000 of 2-year bonds to ensure that the trade was duration neutral. In this case, the cost of carry must be factored into the P&L of the trade.
These trades that require borrowing to finance cash shortfall between the purchase and short sale are said to have negative carry, while trades that have short sell proceeds that exceed the purchase amount are said to have positive carry. Positive carry adds to the P&L because the excess cash can earn interest.
2.3) Butterfly
Professional bond traders also have strategies to deal with perceived anomalies of the yield curve shape. If a trader sees an unusual convex hump in a section of the curve there is a strategy to make a bet that the hump will flatten out. For example, if there is a hump between the 2-year and the 10-year, the trader will take a duration neutral short position in the 3-year and 10-year and buys a treasury in the middle of the range of the same duration. In this example the 7-year would do. If the anomaly was a concave dip in the curve, the trader could buy the short and long-term bond, and sell short the intermediate; however this trade would entail negative carry, so the trader would have to have a strong belief that the anomaly would be corrected and that the correction would cause a considerable change in relative prices. These trades are know as butterfly trades.
"Roll down" explanation sourced from Bondsquawk.
"Roll down" explanation sourced from Bondsquawk.


No comments:
Post a Comment